آموزش تصویری مبحث آمار و احتمال و میانگین ریاضی پنجم

به نام همه ی نام های او

هدف : آشنایی با جمع آوری و نمایش داده ها

اهداف جزئی و رفتاری:

1. داده ها را با روش های مختلف مانند نگاه کردن ، پرسیدن، مراجعه به منابع و اندازه گیری جمع آوری کند.
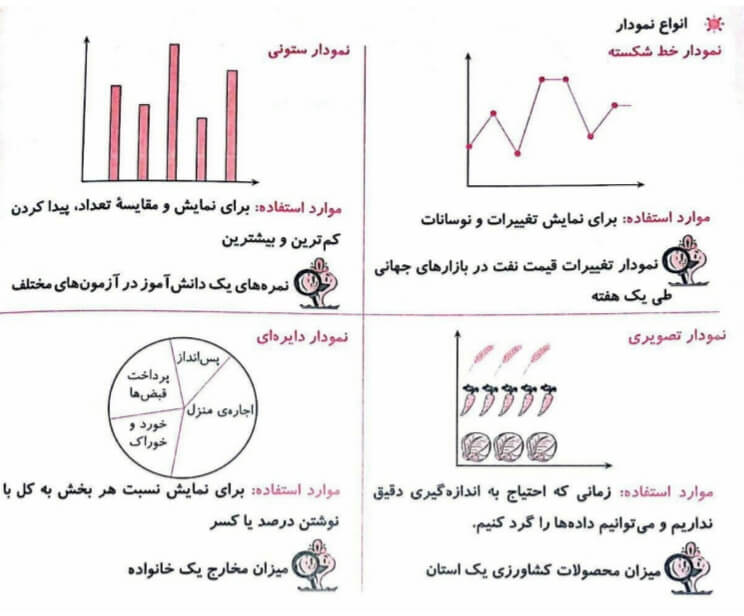
2. از نمودارهای مختلف (ستونی ، تصویری ، خط شکسته و دایره ای)برای نمایش داده ها استفاده می کند.
3. با استفاده از جدول داده ها و نمودارها ، اطلاعات را تفسیر می کند.
4. تفاوت نمودارها و کاربرد هر کدام را می داند.

پیش دانسته ها :
 پایه اول : جمع آوری اطلاعات با چوب خط ، ایجاد آمادگی برای نمودار ستونی
 پایه دوم : سرشماری ، نمودار ستونی و نمودار ستونی
 پایه سوم : جدول داده ها و تفسیر داده ها ، نمودار دایره ای و تبدیل نمودار به یکدیگر
 پایه چهارم : نمودار خط شکسته و تفسیر آن

دانستنی های معلم :

نمودار تصویری: گاهی اوقات به جای داده های واقعی از مقدار تقریبی آن استفاده می کنیم که در برنامه ریزی های کاری نیاز به عددهای واقعی و دقیق نداریم . برای مثال تولید گندم یک استان را به صورت چندهزار تن بیان می کنند یعنی مقدار کمتر از هزار تن در آن بررسی اهمیت ندارد .

در نمودار تصویری نیازمندیم واحدی برای نمایش انتخاب کنیم و با استفاده از این واحد نمودار را تفسیر کنیم و زمانی که احتیاج به اندازه گیری دقیق نداریم و می توانیم داده ها را گرد کنیم قابل استفاده است. همچنین شما میتوانید از آموزش تدریس محیط دایراه که در سایت موجود است نیز دیدن کنید .

نمودار خط شکسته: از نمودار خط شکسته برای بررسی روند تغییرات استفاده می کنند. بنابراین در موضوعاتی که تغییرات اهمیت دارد از این نمودار استفاده می شود به طور مثال در بازارهای مالی ، طلا و… برای نمایش تغییرات و نوسانات قابل استفاده است.

نمودار ستونی: زمانی که قصد مقایسه داده ها و مشخص کردن بیشترین و کمترین داده را داشته باشیم از نمودار از نمودار ستونی استفاده می کنیم که ارتباط بین داده ها را سریع مقایسه می کنیم. برای نمایش و مقایسه تعداد و پیدا کردن بیشترین و کمترین قابل استفاده است.

 نمودار دایره ای یا کیک: نمودار دایره ای از یک دایره تشکیل می شود که نشان دهنده کل است و هر قسمت آن درصدی از کل را نشان می دهد این نمودار عمومیت زیادی دارد زیرا به سادگی قابل تفسیر است و از 100 درصد تجاوز نمی کند. برای نمایش نسبت هر بخش به کل با نوشتن درصد یا کسر قابل استفاده است.

فعالیت پیشنهادی 1:
قبل از ورود به کلاس، روزنامه های موجود را بررسی کنید و یک نمونه اطلاعات را که به صورت جدول داده ها و نمودار آمده است و به کلاس بیاورید .
از دانش آموزان بخواهید که کاربردهایی از علم آمار و نمودار در اطراف خودشان مثال بزنند.

فعالیت پیشنهادی 2:
از دانش آموزان بخواهید که با جست و جو در روزنامه و مجلات ، یک نمودار پیدا کرده و به کلاس بیاورند و در مورد اطلاعات آن به کلاس گزارش دهند. دانش آموزان می توانند کارت رشد خود را( کارت واکسیناسیون .) به کلاس بیاورند و در مورد نمودار خط شکسته و اینکه فراز و فرودهای آن چه چیزی را نشان می دهند گفت و گو کنند.

فعالیت پیشنهادی 3 :
از دانش آموزان بپرسید که می خواهیم ببینیم که دانش آموزان مدرسه کدام شبکه تلویزیون بیشتر دوست دارند ؟ از چه روشی باید استفاده کنیم تا به این سوال پاسخ دهیم؟  (استفاده از نظرسنجی یا پرسش نامه ) . از آنها بخواهید که به صورت گروهی ، هر گروه از یک پایه سوال کنند و نتایج را در جدول داده ها و سپس با انتخاب نمودار مناسب به کلاس گزارش دهند. نتایج هر گروه را در کلاس جمع بندی کنید و جدول داده ها را برای کل مدرسه تهیه کنید .با استفاده از جدول داده ها نمودار ستونی برای شبکه ها و میزان علاقمندان به هر شبکه رسم کنید و از دانش آموزان بخواهید که نمودار را تفسیر کنند .

دست ورزی فصل 7

نمودار ستونی مقایسه میزان آشنایی دانش آموزان کلاس با شماره تلفن های ضروری نوار داده ها متحرک است و روی دو خط افقی و عمودی طلق است که قابل پاک کردن هست.

دست ورزی فصل 7  

نمودار دایره ای نمایش درصد کارهایی که در 24 ساعت انجام شده است .

در آمار ریاضی به اطلاعات جمع آوری شده داده می گویند. اطلاعات جمع آوری شده را در حدودی تنظیم می کنند که به آن جدول داده ها می گویند.

یکی از راه های بررسی داده ها رسم نمودار است.نمودار انواع مختلفی دارد با روش های مختلفی می توان داده ها را جمع آوری کرد مصاحبه ، پرسش ، کتاب و ….

بررسی میزان بارندگی در استان گیلان در شش ماهه دوم

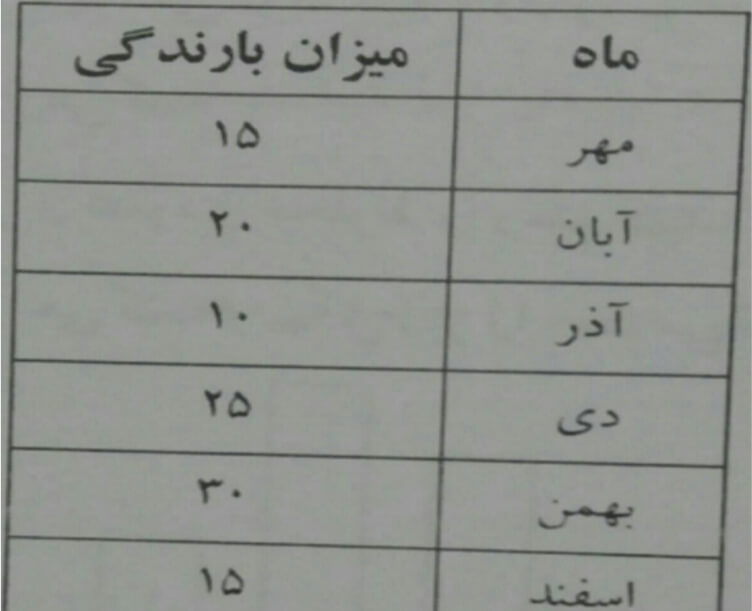
جدول داده ها :

برای نمایش میزان بارندگی و مقایسه و پیدا کردن کمترین و بیشترین بارندگی از نمودار ستونی استفاده می شود.

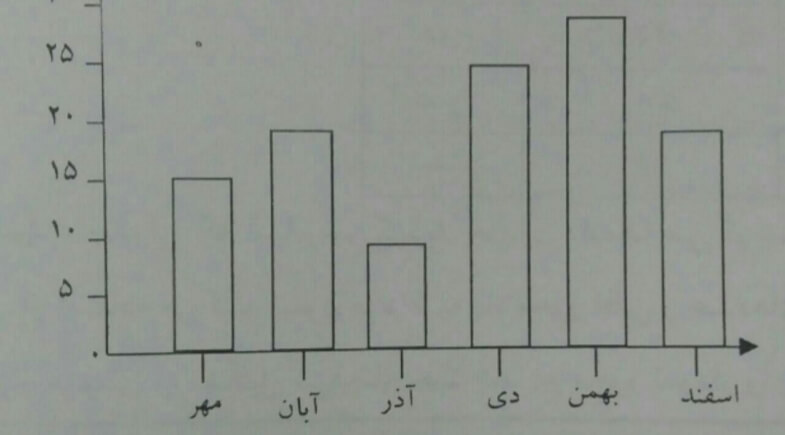
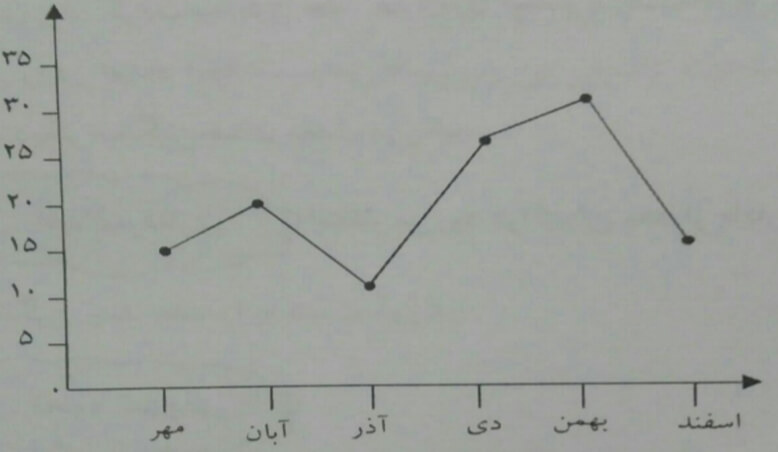
حالا اگر بخواهیم نمایش تغییرات و نوسانات یعنی کم و زیاد شدن بارندگی گیلان در دوره شش ماهه را بررسی کنیم نمودار خط شکسته را رسم کنیم.

مثالی دیگر: جدول داده ها را تهیه می کنیم .از بین 5 نفر میخواهیم اندازه قد آن ها را مقایسه کنیم.

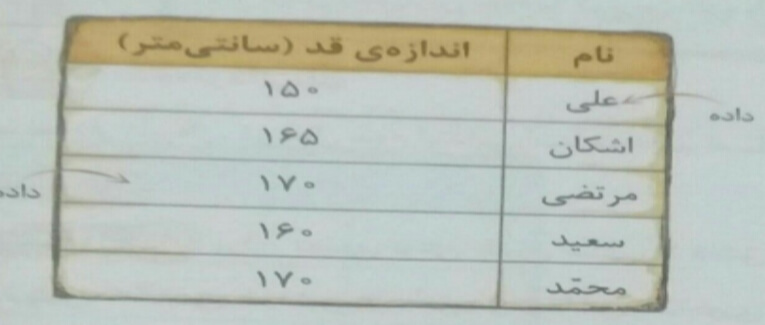
اینجا نمودار ستونی رسم می شود.

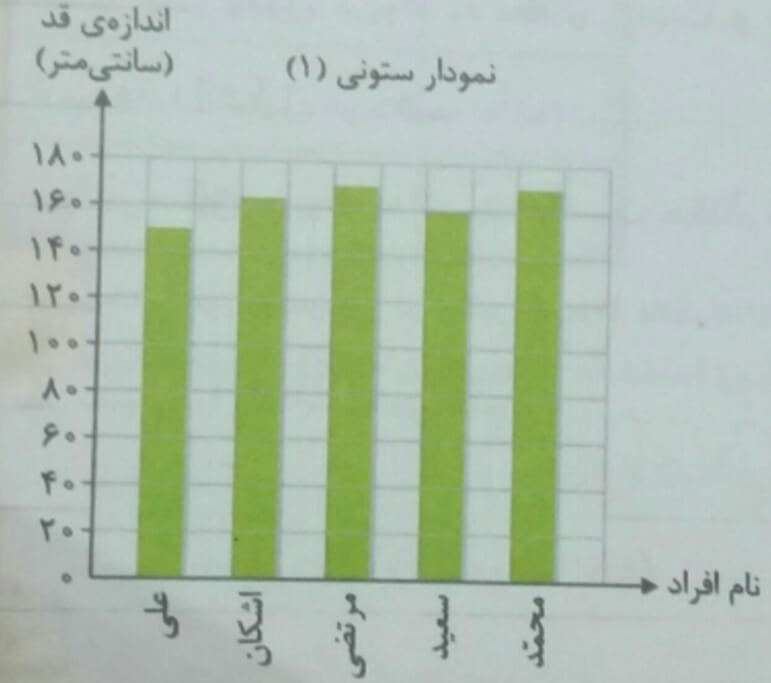
به این نمودار توجه کنید:

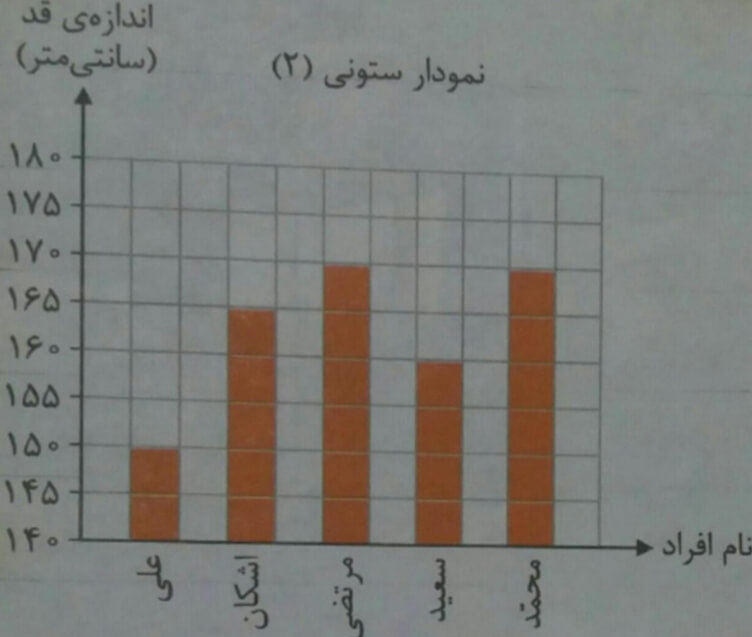
هر دو ستونی رسم شده ولی در نمودار شماره 2 خیلی بهتر میشود قد افراد را مقایسه کرد در نمودار شماره 1 ارتفاع ستون ها خیلی به هم نزدیک است و تقسیم بندی خوب انجام نشده است. با توجه به کمترین داده که 150 است بهتر است تقسیم بندی از عددی کمتر و نزدیک به 150 شروع شود. مثال 140 تا نمایش ساده تر و با دقت تر باشد.
پس از نمودار ستونی هنگامی که بخواهیم داده ها را با هم مقایسه کنیم و به دنبال بیشترین یا کمترین باشیم استفاده می شود.

به جدول داده های زیر دقت کنید:

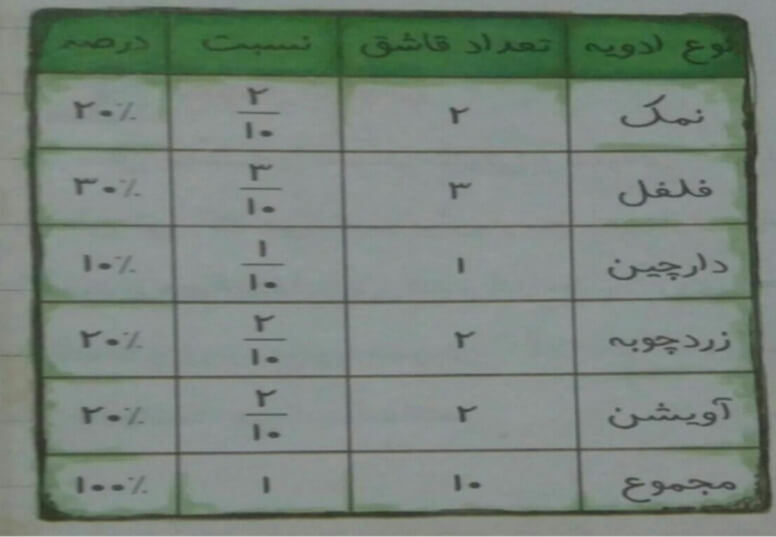
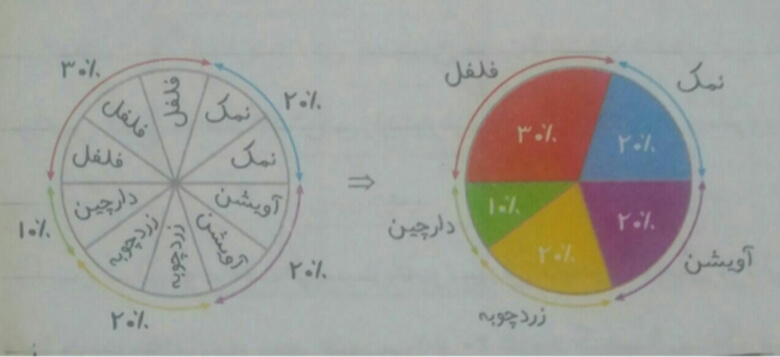
تعداد کل قاشق ها 10 تا است. دایره به 10 قسمت تقسیم می شود. در نمودار دایره ای وقتی دایره را تقسیم بندی کردید در هر قسمت یکی از داده ها به کل آن ها نمایش داده می شود که به صورت درصد بیان می شود. در واقع برای نمایش نسبت هر بخش به کل یا نوشتن درصد استفاده می شود.

نمودار خط شکسته را با مثال دیگر بررسی می کنیم.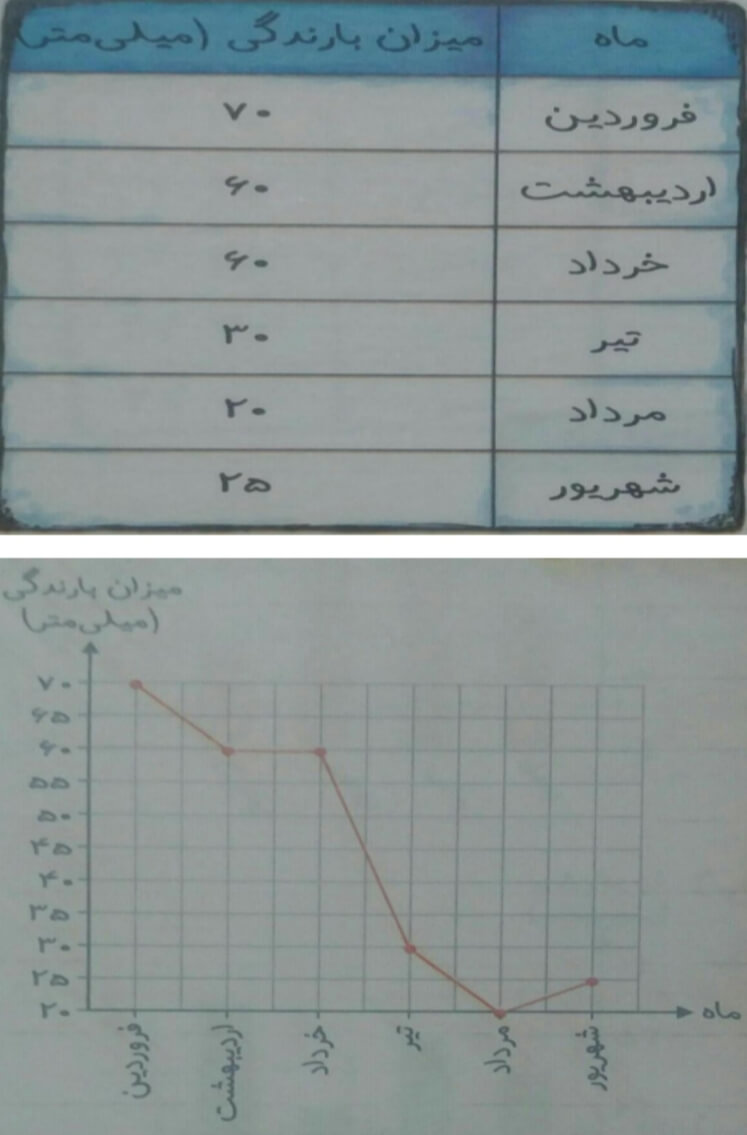

چه اطلاعاتی می توان بدست آورد ؟

در کدام فاصله دو ماهه تغییری در بارندگی نداشتیم؟

در کدام فاصله دو ماهه بارندگی افزایش داشته است؟

بیشترین کاهش بارندگی چه زمانی بوده است؟

اولا از کم ترین بارندگی یعنی 20 تقسیم بندی را شروع کرده تا نمایش بهتر باشد؛ دوما نمودار خط شکسته برای موضوعاتی استفاده می شود که در آن نمایش تغییرات داده ها در طول یک مدت زمانی اهمیت دارد.

ریاضی در زندگی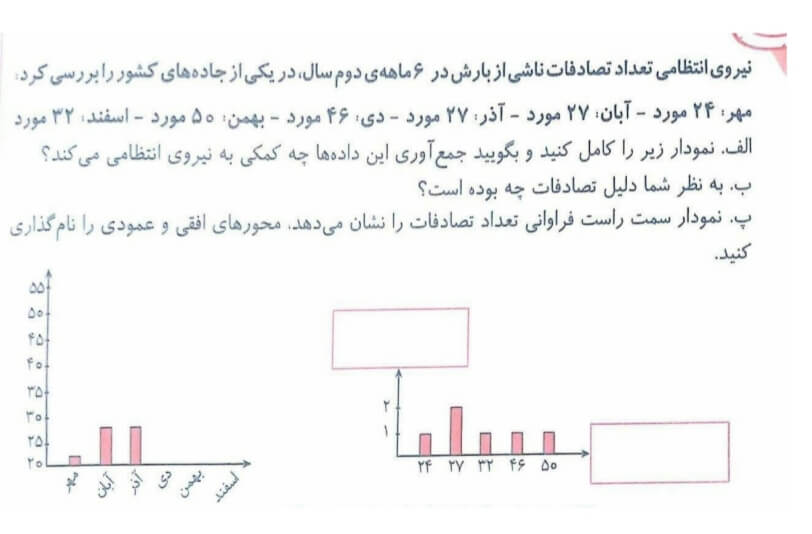قسمت دوم : میانگین

هدف: آشنایی با محاسبه میانگین

اهداف جزیی و رفتاری :
از شاخص های آماری ( بیشترین مقدار ، کمترین مقدار ، میانگین) برای توصیف و مقایسه داده ها استفاده می کند.
مفهوم میانگین را می داند و با بازنمایی هندسی و جبری آن آشنا می باشد.

میانگین دو یا چند داده را محاسبه می کند.

دانستنی های معلم :
هر عددی که برای بیان دسته ای از مقادیر به کار می رود میانگین نامیده می شود .
معدل عبارت است از میانگین عددی و از جمع کردن کلیه مقادیر و تقسیم کردن حاصل بر تعداد کل بدست می آید.

فعالیت پیشنهادی 1:
3 لیوان و یک پارچ به کلاس ببرید.
داخل لیوان ها به اندازه های مختلف آب بریزید .( هر 3 لیوان اندازه مختلف آب داشته باشد و پارچ خالی باشد ). به دانش آموزان بگویید که می خواهیم میزان آب 3 لیوان را با هم برابر کنیم . فکر کنید و یک راه پیشنهاد کنید . راه حل های دانش آموزان را بررسی و با یکدیگر مقایسه کنید. راه حل ها را بررسی و اصلاح کنید که اگر هر 3 لیوان را داخل پارچ ریخته سپس یکی یکی لیوان ها را آب بریزیم و اندازه کنیم در واقع مفهوم جمع داده ها و تقسیم بر تعداد داده ها را کمی بررسی می کنیم.

فعالیت پیشنهادی 2 :

از دانش آموزان بخواهید که با یک کاغذ یک نوار 18 سانتی متری و یک نوار 12 سانتی متری ببرند . اکنون دو نوار را دقیقا کنار هم و بدون فاصله بچسبانید و با خط کش درجه بندی کنید. در مورد پیدا کردن میانگین دو عدد گفت و گو کنید . نوارهای چسبیده به هم را از وسط تا می کنیم و عددی که روی خط تا است را مشخص می کنیم. در مورد ارتباط بین دو اندازه نوار و عدد وسط بررسی کنید و به یک قاعده برسید .

دست ورزی مبحث میانگین – میله وحلقه

به حد متوسط چند مقدار میانگین گفته می شود. برای بدست آوردن میانگین چند مقدار عددها را با هم جمع می کنیم و بر تعداد آن ها تقسیم می شود. در اینجا متوسط ، معدل و میانگین را هم منظور می دانیم.

بررسی تدریس میانگین

به دو دانش آموز مقداری شکلات بدهید.
اولی 7 تا
دومی 19 تا
حالا بگوئید فکر کنن که دانش آموز دومی چند تا شکلات به اولی بدهد تا شکلات ها برابر شود؟

پیشنهادهایی که می توان داشت.

مثال:
یکی یکی از شکالت های نفر دومی برداریم و به اولی بدهیم تا تعداد یکی شود.
اختلافش رو حساب کنیم و تقسیم بر 2 کنیم.
همه رو بریزیم روی هم و یه دفعه تقسیم بر دو کنیم.
حالا با 3 نفر ادامه دهید.
نفر اول 7 سیب
نفر دوم 3 سیب
نفر سوم 5 سیب
می خواهیم کاری کنیم که به هریک از آن ها سیب های مساوی برسد. همه ی سیب ها را روی هم بریزیم و بعد بین سه نفر تقسیم شود.

جابجا کردن 2 سیب از نفر اولی به دومی. پس میانگین سیب ها 5 است. یعنی اگر همه برابر شد همگی دارای 5 سیب خواهند بود. بعد تدریس را با اعداد ادامه دهید.
مثال متوسط عددهای 7و8و9و10و11 را حساب کنید.
7+8+9+10+11=45
45÷5=9

محاسبه میانگین از روی نمودار ستونی داده ها

اگر نمودار ستونی را داشته باشیم می توانیم میانگین داده ها را بدست آوریم. با برش قسمتی از داده ها و اضافه کردن به ستون های دیگر ارتفاع همه ستون ها یکسان می شود.
عددی که هر ستون در حالت برابر شده نشان داد میانگین خواهد بود.

در این نمودار سن 5 نفر از کارمندان یک شرکت نمایش داده شده است. میانگین سن این 5 نفر را حساب می کنیم. وقتی ارتفاع یکی شد ارتفاع همه ستون ها 35 می شود. این یعنی میانگین سن این 5 کارمند 35 سال است.

روش محاسبه

35+37+33+38+32=175
175÷5=35

در بعضی موارد امکان دارد میانگین بصورت اعشار یا کسر بدست آید.

1 1 9 7
1+1+7+9=18
18÷4=4/5

سوالاتی از این قبیل را دقت کنید: سه عدد مثال بزنید که میانگین آن 10 باشد.
یعنی:
جمع اعداد ÷3 = میانگین
جمع اعداد ÷3=10
پس جمع اعداد برابر است
با میانگین × 3
جمع اعداد = 10×3
حالا سه عدد که جمع آنها 30 باشد.
مثال
3 و 20 و 7
10 و 10 و 10
5 و 10 و 15
و …..

سوال دیگر:
میانگین 4 عدد مختلف 10 شده است
اگر بزرگترین 25 باشد کوچکترین 4 باشد.
مجموع دو عدد دیگر را حساب کنید
قرار شد
مجموع 4عدد ÷ 4 = میانگین
مجموع 4 عدد ÷ 4 = ده
مجموع 4 عدد = 40

مجموع 4 عدد =
2+25+مجموع دو عدد دیگر = 40
مجموع دو عدد =
40 – 27=13

روش دیگر برای محاسبه میانگین چند عدد(روش آقای حکیمی)

330 – 340 – 322 – 308
کوچکترین عدد را پیدا کنید : 380
آن را از همه اعداد کم کنید
308 – 308 = 0
322 – 308 = 14
340 – 308 = 32
330 – 308 = 22
حاال میانگین اعداد جدید را حساب کنید
0 + 14 + 32 + 22 = 68
68 ÷ 4 = 17
میانگین این اعداد جدید را با کوچکترین عدد یعنی 308 جمع کنید.
308 + 17 = 325
از روش مجموع امتحان کنید
308 + 322 + 340 + 330 = 1300
1300 ÷ 4 = 325
این همان روش آقای حکیمی صفحه 132 کتاب درسی است.

ریاضی در زندگی

قسمت سوم : احتمال
هدف: آشنایی با کاربرد احتمال و مفاهیم ممکن و غیر ممکن و حتما

اهداف جزیی و رفتاری :
 مفهوم ممکن ، غیر ممکن و حتمی را می داند و مصداق آن را تشخیص می دهد.
 امکان رخ دادن دو اتفاق تصادفی را مقایسه می کند.
 به کمک مقایسه امکان برد و باخت بازی های عادلانه و نا عادلانه را مشخص می کند.

پیش دانسته های دانش آموزان :
 پایه اول : آشنایی با کلمه احتمال در تصویر
 پایه دوم : آشنایی با احتمال در قالب بازی و نمودار ستونی
 پایه سوم : آشنایی با احتمال در قالب کسر و عبارت به طور حتم احتمال می افتد یا احتمال دارد یا به طور حتم اتفاق نمی افتد.
 پایه چهارم : توصیف احتمال با عبارت به طور حتم احتمال می افتد یا به احتمال بیشتر ، به احتمال برابر ، به احتمال کمتر ، به طور حتم اتفاق نمی افتد.

فعالیت پیشنهادی 1 :

در یک کیسه تعدادی مهره قرار دهید . 5 مهره قرمز – 10 مهره آبی
هر بار بدون نگاه کردن به داخل کیسه یک مهره خارج کنید و بعد از یادداشت کردن رنگ آن دوباره مهره را به کیسه برگردانید و پس از 10 بار بیرون آوردن مهره از داخل کیسه احتمال دارد که صفر تا ده بار به رنگ آبی دربیاید. پس از 10 بار بیرون آوردن مهره احتمال دارد که صفر تا ده بار به رنگ قرمز دربیاید. اگر چند بار این فعالیت را انجام دهیم احتمال دارد که جدول ما هر دفعه با جدول قبل متفاوت باشد. اگر چندین بار این فعالیت را انجام دهیم احتمال دارد هر دفعه تعداد رنگ های مهره آبی و قرمز که از کیسه بیرون بیاید با دفعه قبل متفاوت باشد.

فعالیت پیشنهادی 2:
یک سکه بردارید و آن را به هوا پرتاب کنید و هر بار پشت یا رو آمدن آن را یادداشت کنید. این کار را 20 بار انجام دهید و جدول را کامل کنید. جدول خود را با جدول بقیه مقایسه کنید.

فعالیت پیشنهادی 3:
یک تاس را پرتاب کنید و هر بار عددی که ظاهر می شود را یادداشت کنید. این کار را 20 بار انجام دهید و جدول مربوط به آن را کامل کنید. جدول خود را با جدول بقیه مقایسه کنید.
اگر نتیجه آزمایش را از پیش نتوان به طور قطع معین کرد آن را تصادفی می نامیم این آزمایش سکه تصادفی است زیرا قبل از پرتاب سکه نمی توان به طور قطع معین کرد که کدام طرف خواهد آمد و هر بار جدای از دفعه قبل است یعنی نمی توان گفت چون یک بار روی سکه آمده دفعه بعد حتما پشت سکه می آید و نتیجه دفعه اول تاثیری بر نتیجه دفعه دوم ندارد .
در بررسی عادلانه و ناعادلانه بودن بازی ها این نکته اهمیت دارد که اگر برای شرکت کنندگان شانس برابر وجود داشت آن بازی عادلانه است مثال اگر سکه را پرتاب کنیم رو بیاید نفر اول برنده است و اگر پشت بیاید نفر دوم برنده است اما اگر در بازی شانس برابر وجود نداشته باشد آن بازی ناعادلانه است .مثال تاس را پرتاب کنیم و اگر 2 و 3 بیاید نفر اول برابر است و اگر 1 و 4 و 5 و 6 بیاید نفر دوم برنده است.
                                                                                    دست ورزی و انجام بازی عادلانه عملی احتمال

بازی گروهی گردونه ی شانس – ریاضی پنجم – احتمال

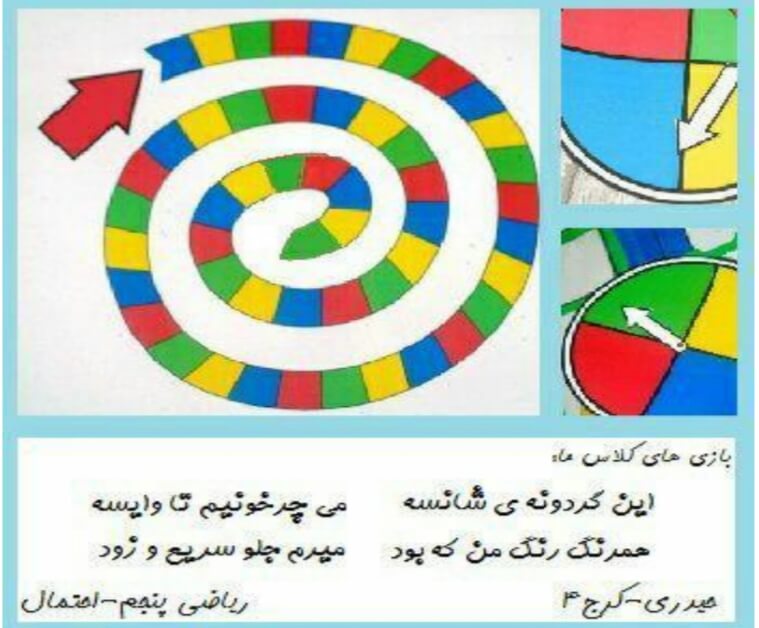
این بازی یک فعالیت جهت ایجاد انگیزه برای فصل 7 ریاضی یعنی مبحث احتمال هست. شعر بالا، روش بازی رو بیان می کنه. یک صفحه ی بازی مارپیچی داریم که برای جذاب شدنش رنگش زدیم. اون رنگ های روی صفحه ی مارپیچی برای قشنگی ظاهری هستش. یک گردونه ی شانس هم داریم که به تعداد اعضای هر گروه رنگ های مختلف داره.
گردونه رو می چرخونند و هر رنگی که ایستاد دانش آموزانی که همرنگ اون هستند اجازه ی جلو بردن مهره شون رو روی صفحه ی بازی خواهند داشت.

الگوی بازی گردونه ی شانس- قابل پرینت

الگوی بازی گردونه ی شانس- قابل پرینت

الگوی بازی گردونه ی شانس- قابل پرینت

تصاویر با کیفیت صفحه ی بازی مار و پله – بازی های شانسی و برپایه ی احتمال؛ استاد حیدری

مبحث احتمال دست ورزی تاس

دست ورزی مبحث احتمال – چرخنده

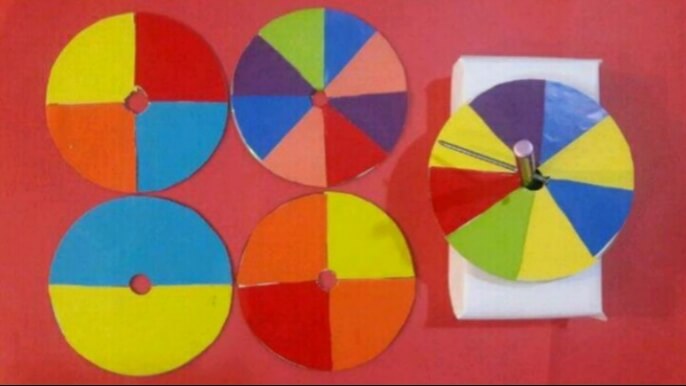
دست ورزی چرخنده آمار احتمال

اینو می چرخونی و بطور تصادفی انگشت رو یه قسمت میزاری و نگهش میداری.

برای بیان احتمال رخ دادن یک اتفاق به عبارت های زیر دقت کنید.

• یک مثلث به طور حتم سه ضلع دارد.
• هوا ابری است به احتمال زیاد باران می بارد.
• من کم درس خواندم احتمال کمی دارد نمره خوبی بگیرم.
• به احتمال برابر در محاسبه قبول می شوم یعنی امکان قبول شدن و قبول نشدن من با هم مساوی است.
• هواپیما تا 5 دقیقه دیگر پرواز می کند احتمال این که بتوانم به فرودگاه برسم غیر ممکن است.

در این کیسه تعدادی مهره آبی و قرمز و سبز وجود دارد. احتمال رخ دادن هر اتفاق در جدول بررسی شده است.

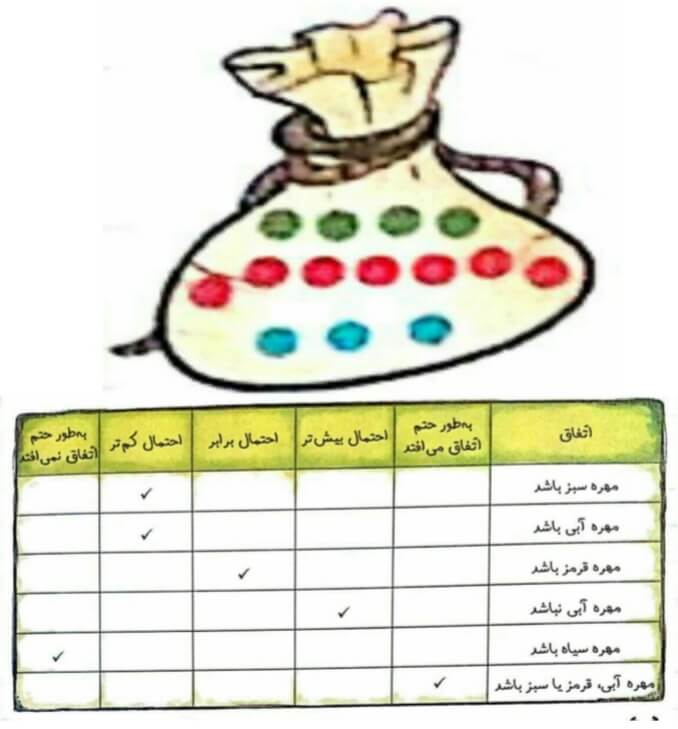
بازی شانسی بازی است که نتیجه و برد و باخت از اول معلوم نیست به بازی های شانسی که احتمال برد وباخت برای طرفین در هر دویکسان باشد یعنی شرایط بازی برای هر دو یکسان باشد بازی شانسی عادلانه می گوییم.
مثال
از کیسه روبرو یک مهره خارج کنید.
اگر قرمز بود اولی برنده است.
اگر سبز بود دومی برنده است.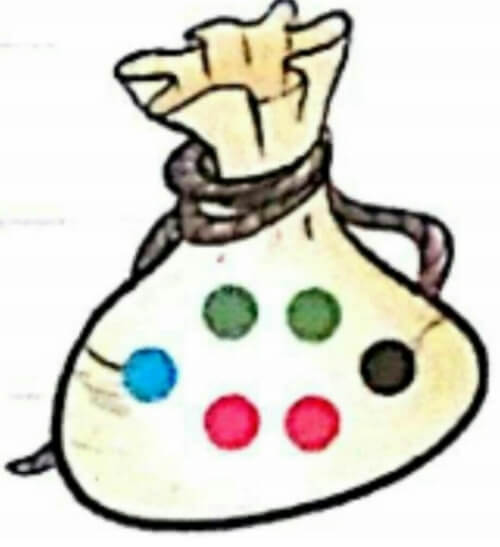

• این بازی شانسی هست، چون نتیجه از اول معلوم نیست .
• عادلانه است، چون هر دو یک مهره خارج می کنند و تعداد مهره قرمز و سبز برابر است.

همین طور در این چرخنده ، قرمز دو تا است و آبی هم معادل دو قسمت. پس شرایط بازی شانسی عادلانه است.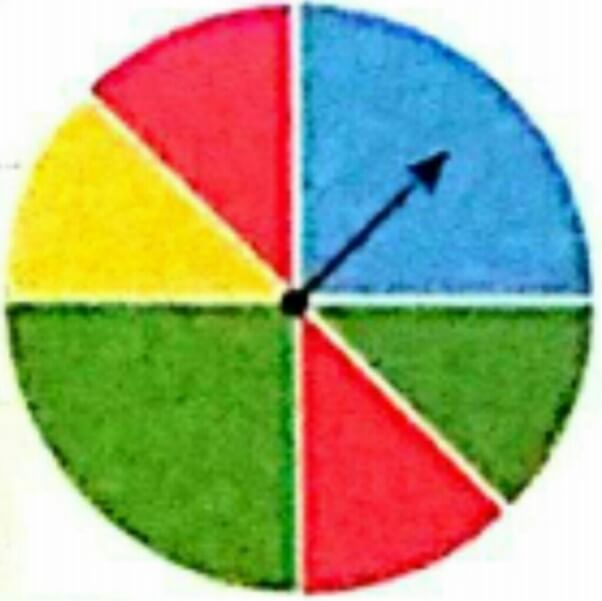نکته:

• احتمال این که فردا ابری باشد : ممکن
• احتمال این که تاس عدد زوج بیاید : برابر
• احتمال این که بعد از چهارشنبه دوشنبه بیاید : غیر ممکن
• احتمال این که تولد کسی 30 اسفند باشد : کم
• احتمال این که در فصل پاییز برگی نریزد : غیر ممکن
• بعد از اردیبهشت خرداد باشد :حتما
• احتمال این که از گندم لوبیا بروید : غیر ممکن
• احتمال این که فردا معلم نیاید: ممکن
• احتمال این که سنگی را به هوا پرتاب کنیم سنگ به زمین بیفتد: حتمی
• احتمال این که سکه رو بیاید : برابر

• حتمی : حتما اتفاق می افتد یعنی 100%
• به احتمال زیاد :  یعنی 50  %اتفاق می افتد مثال در پرتاب تاس عدد 2 یا 3 یا 4 یا 5 بیاید.
• به احتمال کم : کمتر از 50 % باز هم ممکن است اتفاق بیفتد .حتی اگر احتمالش کم باشد مثال در پرتاب تاس عدد 1 بیاید.
• برابر : یعنی پنجاه پنجاه یا 50 % پس احتمال رخ دادن یا رخ ندادن برابر است. در پرتاب تاس عدد زوج یا فرد بیاید.
• غیر ممکن : احتمال صفر امکان ندارد اتفاق بیفتد مثال در پرتاب تاس عدد دورقمی بیاید.

از بین این بازی های شانسی کدام عادلانه است؟

یک سکه را انداخته اگر پشت بیاید بازیکن اول برنده است در غیر اینصورت بازیکن دوم برنده است:
عادلانه است چون احتمال برابر دارد سکه یا رو می آید یا پشت پس احتمال برنده شدن این دو بازیکن برابر است.

یک تاس را می اندازیم اگر 6 بیاید نفر اول برنده است در غیر این صورت نفر دوم برنده است:

عادلانه نیست چون در پرتاب تاس یا عدد 6 و یا یکی از عدد های 1 و 2 و 3 و 4 و 5 می آید پس احتمال این که 6 بیاید ممکن ولی کم است پس احتمال برنده شدن هر دو برابر نیست.

خدا قوت دوستان

سایر مطالب سایت 

نمونه سوالات امتحانی نوبت دوم تمام دروس پایه پنجم اردیبهشت 1400

نحوه ثبت نمرات دانش آموزان در سامانه سیدا 1400-1399

نمونه سوالات درس به درس هدیه های آسمان پایه پنجم ابتدایی اردیبهشت99

نمونه سوالات فصل به فصل و نوبت دوم ریاضی چهارم دبستان

دانلود سوالات امتحانی نوبت دوم تمام دروس پایه اول ابتدایی به صورتpdf

نمونه متن املا و روانخوانی نوبت دوم پایه اول ابتدایی بصورتpdf

دانلود نمونه سوالات امتحانی ریاضی نوبت دوم پایه چهارم به صورتpdf

درسنامه عددهای کسری ریاضی پایه سوم دبستان آذر ماه99

درسنامه اعداد اعشاری فصل سوم ریاضی ششم دبستان آذرماه99

در پناه خدا سالم باشید.